- Home ›
- Java2Dによる画像処理 ›
- 図形の変形 ›
- HERE
拡大縮小について
では次に拡大と縮小です。例えばX軸方向に"2倍"、Y軸方向に"1/2倍"させたい場合には次のような変換行列を設定すればいいことになります。
[ 2 0 0 ] [ x ] [ x' ] [ 0 0.5 0 ] × [ y ] = [ y' ] [ 0 0 1 ] [ 1 ] [ w' ] x' = 2x y' = 0.5y
拡大縮小の場合は簡単ですので自分で設定しても問題ないかと思います。ただメソッドを使った方が簡単は簡単なので拡大縮小についても2つのメソッドを確認してみます。
setToScale
まずsetToScaleメソッドから見てみます。
setToScale
public void setToScale(double sx,
double sy)
この変換をスケーリング変換に設定します。この変換を表現する行列は次のよ
うになります。
[ sx 0 0 ]
[ 0 sy 0 ]
[ 0 0 1 ]
パラメータ:
sx - 座標を X 軸方向にスケーリングするために使う係数
sy - 座標を Y 軸方向にスケーリングするために使う係数
実際に簡単なサンプルを作成して試してみます。縮小させ、その変換行列の値を標準出力に出すようにします。
import java.awt.*;
import java.awt.geom.*;
import java.awt.event.*;
import javax.swing.*;
public class AffineTransformTest extends JPanel{
public static void main(String[] args){
JFrame frame = new JFrame();
AffineTransformTest test = new AffineTransformTest();
frame.getContentPane().add(test);
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.setBounds( 0, 0, 200, 200);
frame.setVisible(true);
}
public void paintComponent(Graphics g) {
Graphics2D g2 = (Graphics2D) g;
g2.draw(new Rectangle2D.Double(60, 20, 60, 40));
AffineTransform af = new AffineTransform();
double[] flatmatrix = new double[6];
af.getMatrix(flatmatrix);
printMatrix(flatmatrix);
System.out.println();
af.setToScale(0.8d, 0.5d);
af.getMatrix(flatmatrix);
printMatrix(flatmatrix);
g2.setTransform(af);
g2.setColor(Color.red);
g2.draw(new Rectangle2D.Double(60, 20, 60, 40));
}
public static void printMatrix(double[] flatmatrix){
System.out.print("[ " + flatmatrix[0] + " ");
System.out.print(flatmatrix[2] + " ");
System.out.println(flatmatrix[4] + " ]");
System.out.print("[ " + flatmatrix[1] + " ");
System.out.print(flatmatrix[3] + " ");
System.out.println(flatmatrix[5] + " ]");
}
}
実行結果は下記のようになります。
[ 1.0 0.0 0.0 ] [ 0.0 1.0 0.0 ] [ 0.8 0.0 0.0 ] [ 0.0 0.5 0.0 ]
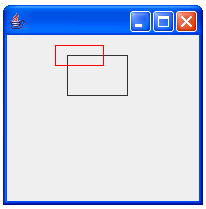
setToScaleの場合には、対象となる変換行列にどのような値が設定されていたとしても完全に新しい行列に置き換えてしまいます。
scaleメソッド
次にscaleメソッドについてです。
scale
public void scale(double sx,
double sy)
この変換をスケーリング変換に連結します。これは、concatenate(S) を呼び
出すことに相当します。ただし、S は次の行列で表現される AffineTransform
です。
[ sx 0 0 ]
[ 0 sy 0 ]
[ 0 0 1 ]
パラメータ:
sx - 座標を X 軸方向にスケーリングするために使う係数
sy - 座標を Y 軸方向にスケーリングするために使う係数
先ほどのsetToScaleの場合は変換行列を完全に置き換えていましたが、scaleの場合は置き換えではなく、既存の変換行列に新たに乗算を行い、その結果を新しい変換行列の値とします。
例えば既存の変換行列が下記左のような行列だった場合、scaleメソッドを実行することで、右の行列のような新しい変換行列になります。
[ m00 m01 m02 ] [ sx 0 0 ] [ m00*sx m01*sy m02] [ m10 m11 m12 ] × [ 0 sy 0 ] = [ m10*sx m11*sy m12] [ m20 m21 m22 ] [ 0 0 1 ] [ m20*sx m21*sy m22]
scaleメソッドでは、実行前と後で変換行列の右側の列は影響を受けません。その為、平行移動に関する値が設定されていた場合にscaleメソッドを実行してもその部分は変化がありません。
では、これも簡単なサンプルで試してみます。
import java.awt.*;
import java.awt.geom.*;
import java.awt.event.*;
import javax.swing.*;
public class AffineTransformTest extends JPanel{
public static void main(String[] args){
JFrame frame = new JFrame();
AffineTransformTest test = new AffineTransformTest();
frame.getContentPane().add(test);
frame.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
frame.setBounds( 0, 0, 200, 200);
frame.setVisible(true);
}
public void paintComponent(Graphics g) {
Graphics2D g2 = (Graphics2D) g;
g2.draw(new Rectangle2D.Double(60, 20, 60, 40));
AffineTransform af = new AffineTransform();
double[] flatmatrix = new double[6];
af.getMatrix(flatmatrix);
printMatrix(flatmatrix);
System.out.println();
af.setTransform(1.0d, 0.0d, 0.0d, 1.0d, 10.0d, 20.0d);
af.getMatrix(flatmatrix);
printMatrix(flatmatrix);
g2.setTransform(af);
g2.setColor(Color.red);
g2.draw(new Rectangle2D.Double(60, 20, 60, 40));
System.out.println();
af.scale(0.8d, 0.5d);
af.getMatrix(flatmatrix);
printMatrix(flatmatrix);
g2.setTransform(af);
g2.setColor(Color.blue);
g2.draw(new Rectangle2D.Double(60, 20, 60, 40));
}
public static void printMatrix(double[] flatmatrix){
System.out.print("[ " + flatmatrix[0] + " ");
System.out.print(flatmatrix[2] + " ");
System.out.println(flatmatrix[4] + " ]");
System.out.print("[ " + flatmatrix[1] + " ");
System.out.print(flatmatrix[3] + " ");
System.out.println(flatmatrix[5] + " ]");
}
}
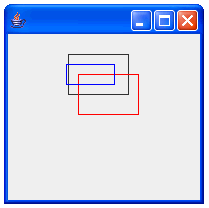
実行結果は下記のようになります。
[ 1.0 0.0 0.0 ] [ 0.0 1.0 0.0 ] [ 1.0 0.0 10.0 ] [ 0.0 1.0 20.0 ] [ 0.8 0.0 10.0 ] [ 0.0 0.5 20.0 ]
( Written by Tatsuo Ikura )

 JavaDrive
JavaDrive